Easing the decision-making process with the AHP matrix
The Analytical Hierarchy Process is a technique to help to organize, analyzing and optimizing complex decisions, and in this entry, I'm going to show you how I implemented it in Python
Taking decisions can become a very complex issue especially in those occasions where the judgment of many people comes into play and when there are many alternatives to evaluate based on a large number of criteria.
How the AHP works
It considers some criteria to base our decisions on, and a set of alternatives
amongst we have to pick up one, or at least rank them in a way that we show
the ones that stick better to these criteria. As some criteria could be
conflicting, in general, the option that will be chosen as the best will not
necessarily perform the best in each criterion, but rather it will have a
"fair" performance in all of them.
It is also true, that the AHP is based on the subjective input of "expert"
evaluators, but different experts might have a different vision on the same
topic, so gathering inputs from many experts is also a way to finally be able
to properly rank the options.
Why implement it in Python?
If this tool is so simple, why is it a good idea to have it implemented in
Python? (or in any other tool such as Excel or Matlab). The way the AHP works
is by establishing a pairwise comparison between alternatives based on the
different criteria, so just considering 3 criteria and 3 alternatives would
require thinking of 180 numbers, filling 5 matrices, and 2 vectors.
And of course, these matrices and vectors need some processing, and this part of the process is the one in which a tool like this one I made comes in handy, it acts as a calculator let's say. The expert judgments cannot be substituted, but the calculations done will help the experts afterward.
Although, the AHP also helps to evaluate the consistency of the inputs
provided by the experts, to avoid considering inputs that are maybe not
thought enough and therefore should be avoided.
The mathematics behind the AHP
I don't want to bore you all so in case you want to learn more about the
mathematics behind it I will leave two papers that have been very useful to
construct the program.
- Relative Measurement and its Generalization in Decision Making, Why Pairwise Comparisons are Central in Mathematics for the Measurement of Intangible Factors, the AHP (https://rac.es/ficheros/doc/00576.PDF)
- The Analytical Hierarchy Process (https://www3.diism.unisi.it/~mocenni/Note_AHP.pdf)
Anyways, I will do a quick summary of the way it works:
- Build the matrix A, in which the criteria are compared pairwise establishing priorities, for instance, Criteria #1 is more important than Criteria #2, and Criteria #2 is extremely more important than Criteria #3.
- Obtain a weights vector (w) to ponderate the final importance of each criterion.
- Build as many matrices B as criteria there are, for instance, if there are 3 criteria there should be 3 matrices B. Then assess answer the following question until you fill the matrices: "how good Alternative #1 sticks Criteria #1 vs. how good Alternative #2 sticks to Criteria #1? and so on and so on systematically.
- Then obtain a score vector S for each matrix B, and construct the score matrix S which is the outcome of putting together all score vectors.
- Finally, get the global score vector v which is the result of multiplying the Score matrix times the weight vector.
I guess this explanation was not very clear so let's illustrate with the
classical example of having to hire an employee or having to choose a
leader.
The number that is placed in every empty slot of the matrices are filled
following this table.
AHP: Chossing a leader
I am just going to give a really brief overview of the thing, if you want to
read the whole problem with the whole explanations visit this link: https://en.wikipedia.org/wiki/Analytic_hierarchy_process_%E2%80%93_leader_example
The classical choosing a leader problem is widely used as an example to
illustrate how the AHP works. The first thing that is needed to do is to
establish the most relevant criteria to take the decision, in the case of the
leader of a company for instance these ones are identified:
- Experience
- Education
- Charisma
- Age
So now we need to establish the importance of each criterion with respect to
each other, and here is where having the AHP automated somewhere comes in
handy. The experts decided to have this matrix.
This would mean that the "Education" criteria are moderately important
compared to the "Experience", the "Charisma" is moderately important too, but
slightly less than the education, and then we have the "Age" which has very
strong importance compared to the "Experience". The "Charisma" is moderately
more important than the "Education" and the "Age" moderately more important
than the "Education" and finally the "Charisma" which has strong importance
compared to the "Age".
Note that comparing each criterion against himself must always result in a 1,
which indicates equal importance, and that the lower part of the matrix is the
inverse of the upper part of it.
It is also very important to establish the inconsistency of the matrix, which
is calculated following a formula that can be found in one of the links above.
The consistency of this matrix is close to zero, it should always be below
0.1, otherwise, it must be thought again.
Then this very same process needs to go on to evaluate each candidate against
another one for a given criterion.
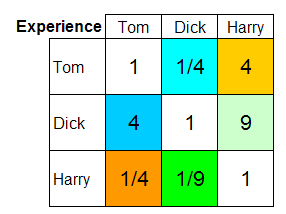
- Regarding experience
The explanation of this matrix goes as follows: Dick's experience is
moderately more important than Tom's, but Tom's is moderately more important
than Harry's. So Dick's experience is extremely more important than Harry's
- Regarding the education
- Regarding charisma
After building all these matrices, they can be introduced in a program like
mine to all the dirty work for you. Here you can see a video of how it works
and a log of its outputs. I will introduce the matrix that appears in the
second paper just so you see how the program works.
As you can see it keeps asking you all the data until all the matrices are
complete, and the output is the score vector, which is then written in an
Excel file so if just one expert is making the judgment. You can see that
alternative number one fits better all criteria, as it rated with 0.52 out of
1 possible points.
However, it would be more useful to have many more inputs from a large number
of experts, in that case, the results file would look like this, where there
are many score vectors where each vector is the result of the judgment of one
expert.
There is a second program that plots this table in columns so it is easier to
visualize the global outcome, but that will come in another entry.
Here you go the code in case you want to take a look at it.
import numpy as np
from sklearn.preprocessing import normalize
import pandas as pd
import os
################## NUMBER OF INPUTS ##################
n_id = int(input("How many inputs will be received?: "))
print("\n")
##################NUMBER OF CRITERIA SECTION##################
m = 0
criteria = []
while ((m <= 2) or (m > 10)):
m = int(input("Enter number of criteria: ")) #Get
the dimension of the matrix A
if(m <= 2):
print("Number of criteria
should be more than 2\n")
elif(m > 15):
print("Number of criteria
should be 15 or less\n")
print("\n")
for i in range(m):
name = input(f"Enter name of Criteria #{i+1}: ")
criteria.append(name)
print("\n")
##################NUMBER OF ALTERNATIVES##################
n = int(input("Enter number of options evaluated: ")) #To get the
dimension of matrix B
print("\n")
alternatives = []
for i in range(n):
name = input(f"Enter name of Alternative #{i+1}:
")
alternatives.append(name)
print("\n")
##########FILL MATRIX 'A' AND CHECK CONSISTENCY##################
matrix_results = np.zeros((n_id,n))
for h in range(n_id):
print("####################")
print(f"DATA FOR RESPONSE #{h+1}")
print("####################")
print("\n")
CI_RI = 3
while (CI_RI > 0.1):
a_1 =
np.zeros((m,m)) #Empty matrices of zeros to then fill
matrix A
a_2 = np.zeros((m,m))
S_big = np.zeros((n,m))
for i in
range(m): #loop to fill upper half of
matrix A
for
j in range(m):
if
(i == j):
a_1[i,j]
= 1 #keep the diaganol to ones
elif
(j > i):
compare
= input(f"Importance of {criteria[i]} compared to {criteria[j]}?: ")
#insert values to compare
a_1[i,j]
= compare
else: #lower
half is zero
a_1[i,j]
= 0
for i in
range(m): #loop to fill lower part of
the matrix
for
j in range(m):
if
(i == j or j > i): #if we are in the upper part then
do nothing
a_2[i,j]
= 0
else:
a_2[i,j]
= 1/a_1[j,i] #if we are in the lower half grab the values previously
introduced and inverse them
A = a_1 + a_2 #join both
matrices to obtain the matrix A with both halves completed
A_norm = normalize(A,
axis=0, norm='l1') #normalization to get the all the columns sum equal to
one
print("\n")
print(f"Matrix A: \n")
print(A)
print("\n")
w = np.zeros(m)
#weights vector calculation, first predimension an
empty array
for i in
range(m): #compute
the weight vector as the sum of each row over the number of criteria
considered
row
= sum(A_norm[i,:])
w[i]
= row/m
w_t = np.transpose(w)
x =
(np.sum(np.divide(np.matmul(A,w_t),w_t)))/m #computes the lambda parameter
CI = round((x-m)/(m-1),3)
print(f"Inconsistency
Index: {CI}")
RI =
{ #Random index
values
2: 0,
3: 0.58,
4: 0.9,
5: 1.12,
6: 1.24,
7: 1.32,
8: 1.41,
9: 1.45,
10: 1.51
}
print(f"Random Index:
{RI.get(m)}")
CI_RI =
round(CI/(RI.get(m)),3)
print(f"CI/RI: {CI_RI}")
print("\n")
if(CI_RI > 0.15):
print("Criteria
matrix is inconsistent and should be redone")
print("\n")
elif((CI_RI > 0.1) and
(CI_RI < 0.15)):
c
= input("Criteria matrix is slightly inconsistent. Do you want to proceed
anyway?[y/n]:")
print("\n")
if
(c == "y"):
print("Criteria
matrix accepted")
print("\n")
break
elif(c
== "n"):
print("Criteria
matrix rejected, redo the matrix")
print("\n")
else:
print("Redo
the matrix")
print("\n")
elif(CI_RI <= 0.1):
print("Matrix
A is consistent enough")
print("\n")
for k in range(m):
B_1 = np.zeros((n,n))
B_2 = np.zeros((n,n))
for i in range(n):
for
j in range(n):
if
(i == j):
B_1[i,j]
= 1 #keep the diaganol to ones
elif
(j > i):
compare
= input(f"How good is {alternatives[i]} vs {alternatives[j]} attending to
{criteria[k]}: ") #insert values to compare
B_1[i,j]
= compare
else: #lower
half is zero
B_1[i,j]
= 0
for i in
range(n): #loop to fill lower part of
the matrix
for
j in range(n):
if
(i == j or j > i): #if we are in the upper part then
do nothing
B_2[i,j]
= 0
else:
B_2[i,j]
= 1/B_1[j,i] #if we are in the lower half grab the values previously
introduced and inverse them
print("\n")
B = B_1 + B_2
print(f"Matrix B_{k+1}: ")
print("\n")
print(B)
print("\n")
B_norm = normalize(B,
axis=0, norm='l1')
s = np.zeros(n)
for i in range(n): #keep
adding s vector to the S matrix
row_new
= sum(B_norm[i,:])
s[i]
= row_new/n
S_big[:,k] = s
print(f"Weights vector w for response #{h+1}:")
#Print the vector of weights
print("\n")
print(w)
print("\n")
print(f"Score Matrix S for response #{h+1}:")
#print the score matrix S
print("\n")
print(S_big)
print("\n")
v = np.matmul(S_big,w) #computes the score vector
print(f"Global Score vector for response
#{h+1}:\n")
print(v)
print("\n")
matrix_results[h,:] = v
print("\n")
#print(matrix_results)
print(matrix_results)
#Exporting to xls file for postprocessing
results_data = pd.DataFrame(matrix_results)
results_data.columns = alternatives
filepath = os.path.join(os.getcwd(), "results.xlsx")
results_data.to_excel(filepath, sheet_name="results",index = True,
header=True)
I hope you liked this more dense entry,
:D








Comments
Post a Comment